01. 과적합(overfitting)

📍과적합(overfitting)이란 무엇이고, 과적합이 발생했을 때 어떠한 방식으로 해결할 수 있는가?
'과적합(overfitting)'은 모델이 학습 데이터에만 지나치게 최적화되어, 학습에 사용되지 않은 새로운 데이터에 대해서는 성능이 떨어지는 현상을 의미한다. 예를들어 토익 시험을 보기 위해 한 권의 문제집으로 영어를 공부하는 학생이 있다고 가정한다. 문제집에 나와있는 모든 문제를 거의 외우다시피 공부한 학생은 다시 그 문제집에 있던 문제를 풀었을 때 100점이 나온다(즉, 학습성능이 높다). 하지만 문제집에 없던, 처음 보는 문제들이 가득한 실제 토익 시험에서는 성적이 떨어지게 되고 이를 일반화 성능이 낮다고 표현한다. 이처럼 모델이 주어진 학습데이터만을 너무 과하게 학습한 나머지, 학습성능은 좋지만 일반화 성능은 떨어지는 것을 오버피팅문제라고 한다. 우리는 train set에 대해서만 성능이 높은 모델을 필요로하는것이 아니라 실제 현장에서 사용할 수 있는 모델을 만드는 것이 목적이므로 오버피팅이 발생되지 않게 하는 것이 중요하다.

딥러닝 모델에서 과적합이 발생되었을때 해결할 수 있는 방법은 다음과 같다
1) 데이터의 양을 늘리기
2) 모델의 복잡도 줄이기
3) 드롭아웃(dropout)적용하기
4) 가중치 규제(Regulation) 적용하기
02. 불균형 데이터(imbalanced data), 샘플링(sampling)

📍데이터의 불균형을 해결하는 방법은 무엇인가?
현실에서는 데이터의 비율이 깨져있는 경우가 아주 많다. 데이터의 비율이 깨져있다는 것은 y가 범주형인 데이터에서, 각 클래스에 속한 데이터의 개수가 너무 심하게 차이 난다는 의미이다. 예를 들어, 어떤 병원에서 100000명의 환자들을 대상으로 유방암이 양성인지 음성인지 라벨링 한 데이터가 있다고 가정했을 때, 수집된 데이터에는 유방암이 양성인 사람보다 음성인 사람의 비율이 훨씬 높을 것이다.
이렇게 불균형 데이터로 모델이 학습하게 되면 예측 결과가 왜곡될 수 있다. 위의 예시에서 유방암에 대해 양성과 음성의 비율이 1:9로 분포되어 있다면, 모델은 유방암이 음성인 데이터를 주로 학습하게 될 것이고, 양성인 경우에 대해서는 제대로 학습하지 못할 가능성이 크다. 따라서 이러한 불균형한 데이터셋을 처리하는 것은 매우 중요하다.
딥러닝에서 데이터 불균형 문제를 해결하는 기본적인 방법은 크게 두 가지로 나눌 수 있다.
1) 샘플링 기법
- 오버샘플링(Oversampling)
: 오버샘플링은 불균형 데이터셋(imbalanced dataset)에서 소수의 클래스(minority class)의 데이터를 증가시켜 각 클래스의 비율을 맞추는 방법이다. 오버샘플링 방법으로는 크게 두 가지가 있는데 1) 데이터를 복제하거나 2) 합성을 생성하는 방법이 있다. 단순 복제 방법은 데이터를 그대로 복제하여 데이터셋을 증가시키는 방법이다. 이 방법으로 오버샘플링을 하게 되면 적용자체는 쉽지만 단순히 중복해서 데이터를 추가하는 것이기 때문에 모델이 과적합(overfitting)될 위험이 있다. 두 번째로 합성 데이터 생성은 소수 클래스에 해당하는 데이터를 이용하여 노이즈를 추가하거나, 회전, 이동 등의 변형을 적용하여 새로운 데이터를 생성하는 방법이다. 이는 모델이 다양한 패턴을 학습하도록 도와주므로 과적합을 방지할 수 있다.
- 언더샘플링(Undersampling)
언더샘플링은 오버샘플링과 반대로, 클래스 중 데이터의 수가 많은 클래스에 해당되는 데이터에서 일부만을 선택하여 데이터셋을 줄이는 방식이다. 언더샘플링을 하면 데이터셋의 크기가 줄어들기 때문에 클래스 간 비율을 어느 정도 맞출 수 있다. 언더샘플링은 무작위로 다수 클래스 데이터 중 일부를 선택하여 데이터셋을 줄이는 방법도 있고, 중요한 정보를 담고 있는 데이터들을 우선적으로 선택하여 데이터셋을 줄일 수 있다. 하지만 언더 샘플링을 할 때 너무 많이 하게 되면 중요한 정보를 손실할 가능성이 높으므로 주의가 필요하다.
2) 가중치 조정
가중치 조정은 소수 클래스의 오분류 비용을 더 크게 설정하여 모델이 소수 클래스에 더욱 민감하게 학습하도록 하는 방법이다.
03. 활성화 함수(activation function)

📍활성화 함수가 무엇이며, 왜 필요한가?
딥러닝 모델은 여러 개의 레이어(layers)로 구성되어 있으며, 각 레이어는 선형 연산과 활성화 함수를 반복적으로 거치게 된다. 이때 활성화함수는 이전층(layer)의 결괏값을 변환하여 다른 층의 뉴런으로 신호를 전달하는 역할을 한다. (쉽게 말해, 활성화함수는 어떠한 input이 들어왔을 때 그 값을 다음 단계로 넘길지 말지, 넘긴다면 얼마큼/어느 값으로 넘길지를 판단하고 실행하는 역할이라고 보면 된다.)
활성화 함수가 필요한 이유는 모델의 복잡도를 증가시키기 위함이다. 만약 인공신경망에 비선형성을 부여해 줄 수 있는 활성화함수가 없다면, 아무리 레이어를 깊게 쌓아도 그 모델은 선형 함수의 조합으로 표현될것이다. 즉 하나의 layer로 구성된 네트워크와 다를바가 없어지며 이러한 선형 함수만을 가지고는 복잡한 문제들을 풀 수 없다. 하지만 우리가 실제적으로 풀고 싶은 문제들은 단순한 형태가 아닌 아주 복잡한 형태의 문제들이기 때문에, 모델에 비선형성을 부여해줄 필요가 있다. 따라서 활성화함수를 사용하여 비선형 문제를 해결할 수 있도록 하는 것이다.(활성화 함수가 없으면 input값을 그대로 다음 레이어로 전달만 하는 구조가 된다. 하지만 뉴런에서 다음 뉴런으로 정보(값)를 전달할 때 값을 그대로 전달하는 게 아니라 '정보의 재해석'을 해주면서 전달해야 하는데 이 정보의 재해석을 해주는 역할이 바로 활성화 함수인 것이다.) 또한 선형함수의 도함수는 상수이므로 입력x와 아무 상관이없다. 때문에 역전파 계산 시 기울기도 항상 동일한 값이 된다. 기울기가 항상 동일한것이 문제가 되는 이유는 오차를 줄일 수 없기 때문이다. 이러한 이유들로 활성화 함수를 사용해야하는것이다.
📍활성화 함수의 종류와 특징을 간단히 설명해 본다면?
1) 시그모이드(Sigmoid)/로지스틱 함수

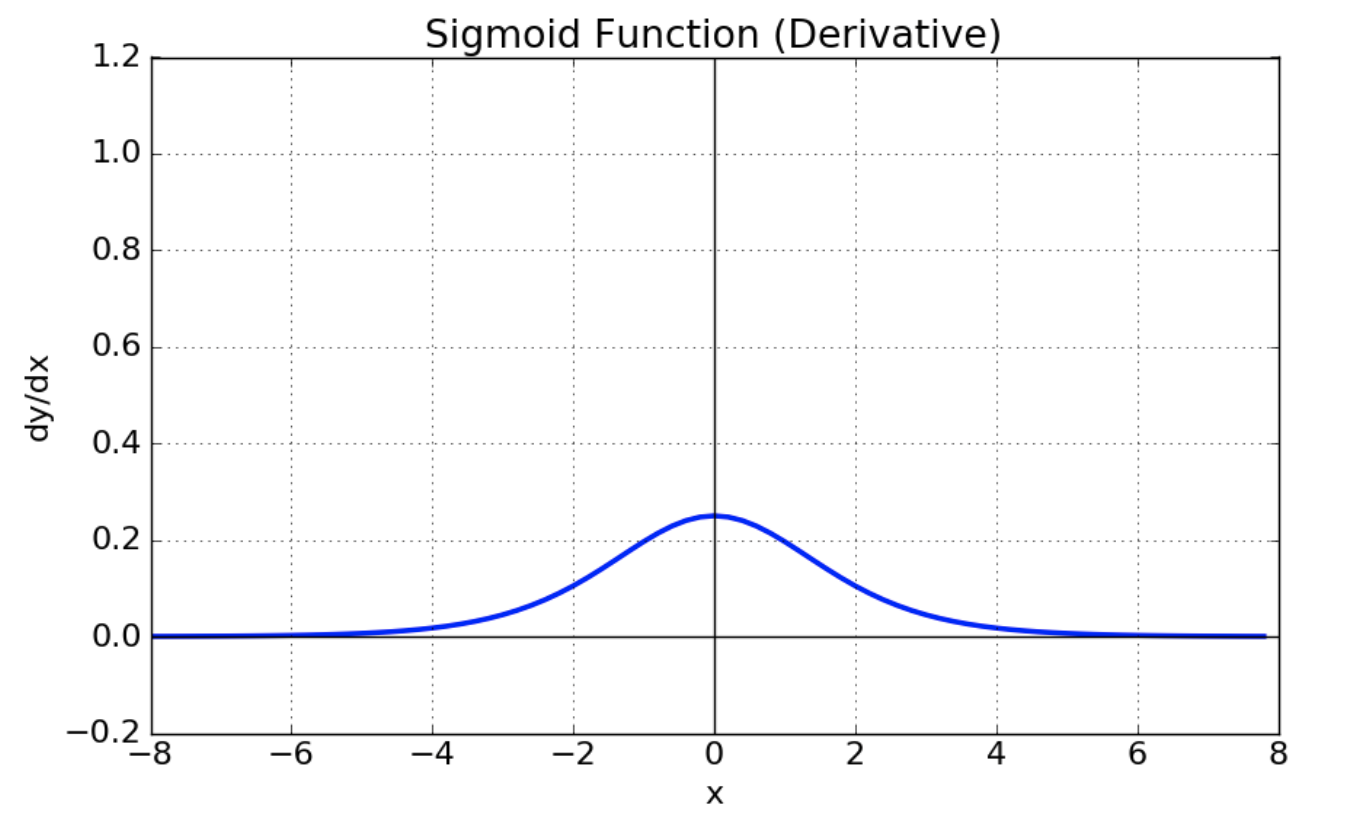
시그모이드 함수는 input 값을 받아 0~1 사이의 범위로 반환하기 때문에 이진분류에서 두 클래스의 확률을 구할 때 사용된다.(이와 비슷하게 소프트맥스 함수는 3개 이상의 클래스를 대상으로 한 분류에서 각 클래스의 확률을 구할 때 출력층의 활성화함수로 많이 사용된다.) 이때 input값의 절댓값이 커질수록 도함수가 0에 가까워지기때문에 역전파 과정에서 기울기 소실 문제를 발생시킬 수 있다.
2) tanh 함수


tanh함수는 input값을 받아 -1에서 1사의 값으로 반환한다. 시그모이드 함수와 마찬가지로 tanh함수도 input값의 절대값이 커질수록 미분값이 0에 가까워진다. 이는 경사하강법을 이용한 학습이 느려진다는 의미로 해석할 수 있다.
3) ReLu 함수

ReLU함수는 input이 0보다 크면 그 값을 그대로 출력하고, 그렇지 않으면(0~음수) 값을 발화하지 않는다. 때문에 대부분 은닉층에서는 기울기 소실문제를 해결하기 위해 활성화 함수로 ReLU를 사용한다.
04. 경사하강법

📍경사하강법에 대해 설명해 본다면?
경사하강법(Gradient Descent)은 함수의 기울기(Gradient)를 이용하여 Global minimum을 찾는 최적화 알고리즘이다. 쉽게 말하자면, 가중치를 반복적으로 수정하며 오차 함수의 최저점에 도달할 때까지 '오차함수'라는 산을 내려가는 과정이라고 볼 수 있다. golbal minumum을 찾아가는 과정에서 기울기를 활용하기 때문에 경사하강법은 미분이 가능한 함수에서 사용가능하며, 경사 하강법을 수행하는 방법은 크게 3단계로 나눌 수 있다.
1) 초기값 설정 : 함수의 최솟값을 찾기 위한 출발점으로서, 일반적으로는 무작위로 설정된다.
2) 기울기 계산 : 1) 번에서 무작위로 설정된 출발점에서의 미분값(기울기)을 계산한다.
3) 위치 업데이트 : 해당 위치에서 기울기를 계산했으면 어느 방향으로 이동할지 정하고 이동하게 된다. 이때 이동할 방향은 기울기에 따라 결정되며 얼마큼의 보폭으로 이동할지는 학습률(learning rate)로 결정된다. 이때 학습률이 너무 크면 최적값에 수렴하지 못하고 발산되며, 학습률이 작으면 너무 조금씩 이동하기 때문에 수렴하는 시간이 오래 걸릴 수 있다.
참고) cost function
https://bigdaheta.tistory.com/85
비용함수(Loss function/cost function)와 경사하강법(Gradient Descent)이란
00. 모델링(Modeling) 머신러닝과 딥러닝의 기본적 컨셉은 대용량의 데이터를 가지고 모델을 만들고, 이 모델에 새로운 데이터를 적용시켰을 때 예측을 잘하도록 하는 것이다. (결국 과거의 데이터
bigdaheta.tistory.com
05. 기울기 소실 문제(Vanishing Gradient Problem)

📍 기울기 소실(Vanishing Gradient)이란 무엇이고 어떻게 해결할 수 있나?
인공신경망에서 학습은 다음의 세 단계를 반복하며 이루어진다
1) 순방향 계산 : 선형 결합(가중합)을 계산하고, 이를 활성화 함수에 입력해서 출력값을 계산한다
2) 출력값과 정답을 비교해서 오차함수/손실함수를 계산한다
3) 경사하강법 알고리즘을 이용해서 오차함숫값을 최적화한다.
이때 역전파 알고리즘을 통해 가중치를 업데이트하게 되는데, 역전파(backpropagation)는 가중치에 대한 오차의 미분을 출력층에서부터 첫 번째 층까지 전달하는 것을 의미한다. 역전파 계산을 통해 가중치가 수정되며 이 과정을 통해 오차함수라는 산을 한걸음 내려오게 되는 것이다. 그리고 1번부터 3번의 과정을 계속 반복하면서 오차함수의 global minimum에 도달하게 된다.
은닉층(hidden layer)이 많은 신경망에서 주로 발생하는 기울기 소실(Vanishing Gradient) 문제는 출력층에서 은닉층으로 전달되는 오차가 크게 줄어 학습이 제대로 되지 않는 현상을 의미한다. 즉, 역전파 과정에서 기울기가 소멸어 학습되는 양이 '0'에 가까워져 학습이 더디게 진행되고 오차를 더 줄이지 못하는 현상이다.
이러한 기울기 소실(Vanishing Gradient Problem)을 해결하기 위해 시그모이드(sigmoid)나 하이퍼볼릭 탄젠트 함수 대신 렐루(ReLU) 활성화 함수를 사용하면 문제를 해결할 수 있다. 하지만 모든 경우에서 ReLU를 사용하는 것이 정답은 아니다. 예를들어, 시계열 데이터의 경우 활성화함수를 ReLU를 사용하는것이 적합하지 않을 수 있다. 그 이유는 ReLU는 input값이 음수인 경우 항상 0 을 출력하기 때문이다. 시계열 데이터는 일반적으로 음수값도 포함되어 있기 때문에 ReLU를 적용하면 정보 손실이 발생될 수 있다. 따라서 시계열 데이터에서는 주로 tanh함수를 사용하는것이 적합하다. 이처럼 데이터와 모델의 특성에 맞게 활성화 함수를 선택하는 것이 중요하다.
'🤖딥러닝' 카테고리의 다른 글
| CalibratedClassifierCV python code (0) | 2024.01.29 |
|---|---|
| [논문 리뷰] Prediction of white-coat hypertension and white-coat uncontrolled hypertension using machine learning algorithm (0) | 2023.06.03 |
| [딥러닝] 선형대수(1) 벡터와 벡터의 기하학적 의미 (0) | 2023.03.15 |
| 비용함수(Loss function/cost function)와 경사하강법(Gradient Descent)이란 (1) | 2023.02.26 |
| Sleep-EDF dataset (python에서 EDF 포맷 읽기) (2) | 2022.11.20 |


