📌 C4.5
C4.5는 불순도 알고리즘으로 엔트로피(Entropy)를 사용한다. 엔트로피는 본래 열역학에 쓰이는 개념으로 '무질서한 정도'를 나타내는 지표로, 의사결정나무에서 지니지수와 비슷한 개념으로 사용된다. 따라서 지니지수와 마찬가지로 엔트로피 값이 작을수록 순수도가 높다고 해석하면 된다. (값이 작을수록 같은 특성을 가진 객체들로만 잘 분류했다는 의미)
➰ 엔트로피 (Entropy)

지니지수의 최댓값은 0.5였다면, 엔트로피 지수의 최대 값은 1이다.
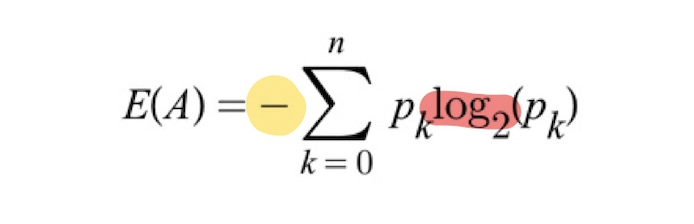
위의 공식을 보면 알 수 있듯, 엔트로피는 로그(log)를 사용하여 계산한다. 그런데 왜 - log로 계산하는 것일까? 엔트로피는 정보이론에서 나왔는데, '정보 이론'은 정보량이 얼마나 많은지 계산하는 이론이다. 컴퓨터는 bit(0과 1)로 구성되어 있기 때문에 log2(로그 2)에 어떤 값을 넣어 불확실성과 정보량을 계산하는 원리인 것이다. 따라서 엔트로피를 계산할 때 (-)가 붙은 이유는 전체 개수 중에 속해있는 개수를 구하다 보니 (pk) 부분이 항상 분수 형태가 나오게 되고, 거기에 로그를 붙이면 항상 (-)로 값이 나오기 때문에 (+)로 전환하기 위해 앞에 (-)를 붙여주는 것이다.
➰ 정보 이익 (IG : Information Gain)
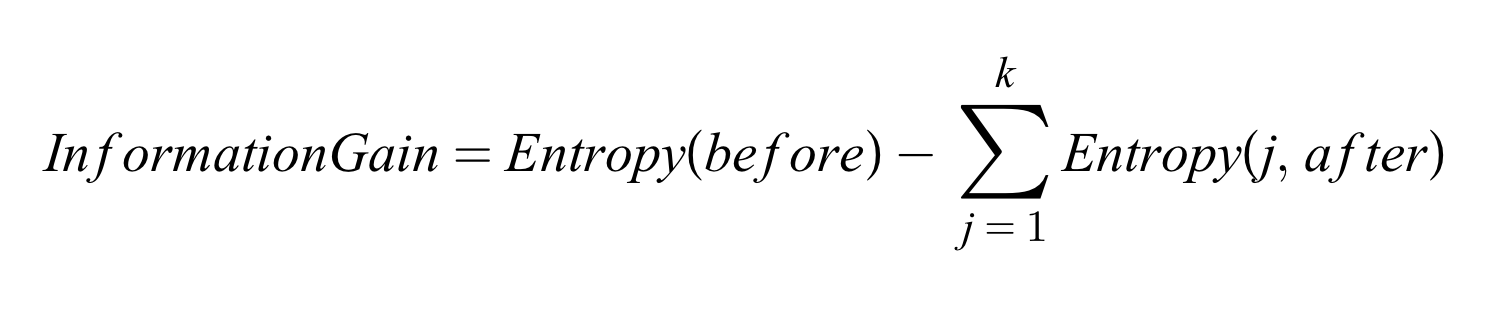
엔트로피 개념을 이용하여 '정보 이익'이라는 개념을 만들 수 있는데, 정보 이익은 정보의 가치를 의미하며 그 값이 클수록 좋다. 위의 계산식을 보면 정보 이익(IG)은 '사전 엔트로피(불확실성)'에서 '사후 엔트로피(불확실성)'을 뺏 값이다. 따라서 IG는 '불확실성이 얼마나 줄어들었는가?'로 해석할 수 있으며, 이 값이 크다는 것은 불확실성이 많이 감소했다는 것을 의미한다.
➰ 이득율 (IGR : Information Gain Ratio)
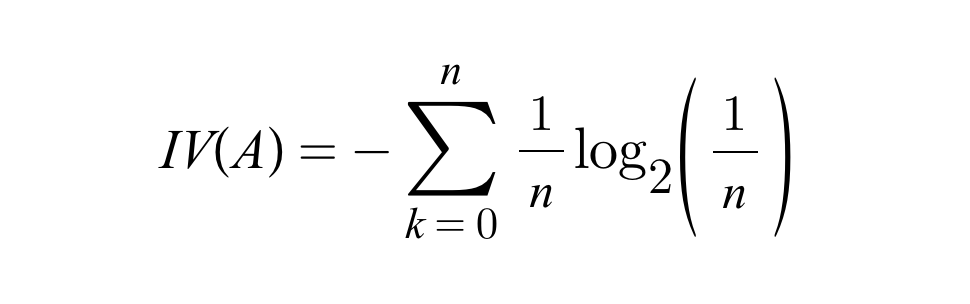
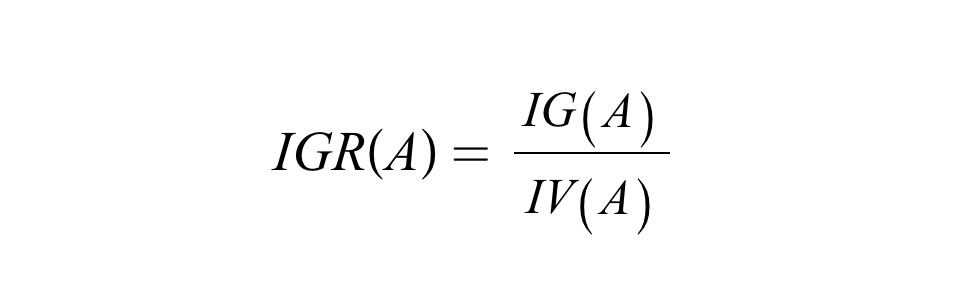
그런데 위의 정보이익을 개념을 사용했을 때 한 가지 문제가 발생한다. 그 이유는 CART에서는 이지 분리(가지가 2개)를 하지만, C4.5에서는 다지 분리로 여러 개의 가지를 생성할 수 있기 때문이다. 이렇게 가지의 개수가 많아지면 가지가 많은 쪽을 더 중요한 분류 기준으로 생각하여 선택하는 문제점이 발생하게 된다. 따라서 이러한 문제점을 보완하기 위해 이득률(Information Gain Ratio)을 사용하게 되었다. 이득률은 정보 이익(IG)을 IV(Intrinsic Value)로 나눈 값으로, IV에 개수를 넣어 그 개수에 따라 페널티를 부여하는 원리이다. 따라서 IGA를 사용하게 되면 페널티에 따라 값이 조금씩 조정되어 IG의 단점을 보완해줄 수 있다.
➰ 엔트로피 예시
지니 지수에서 사용한 예시를 엔트로피를 이용하여 다시 계산해보자.
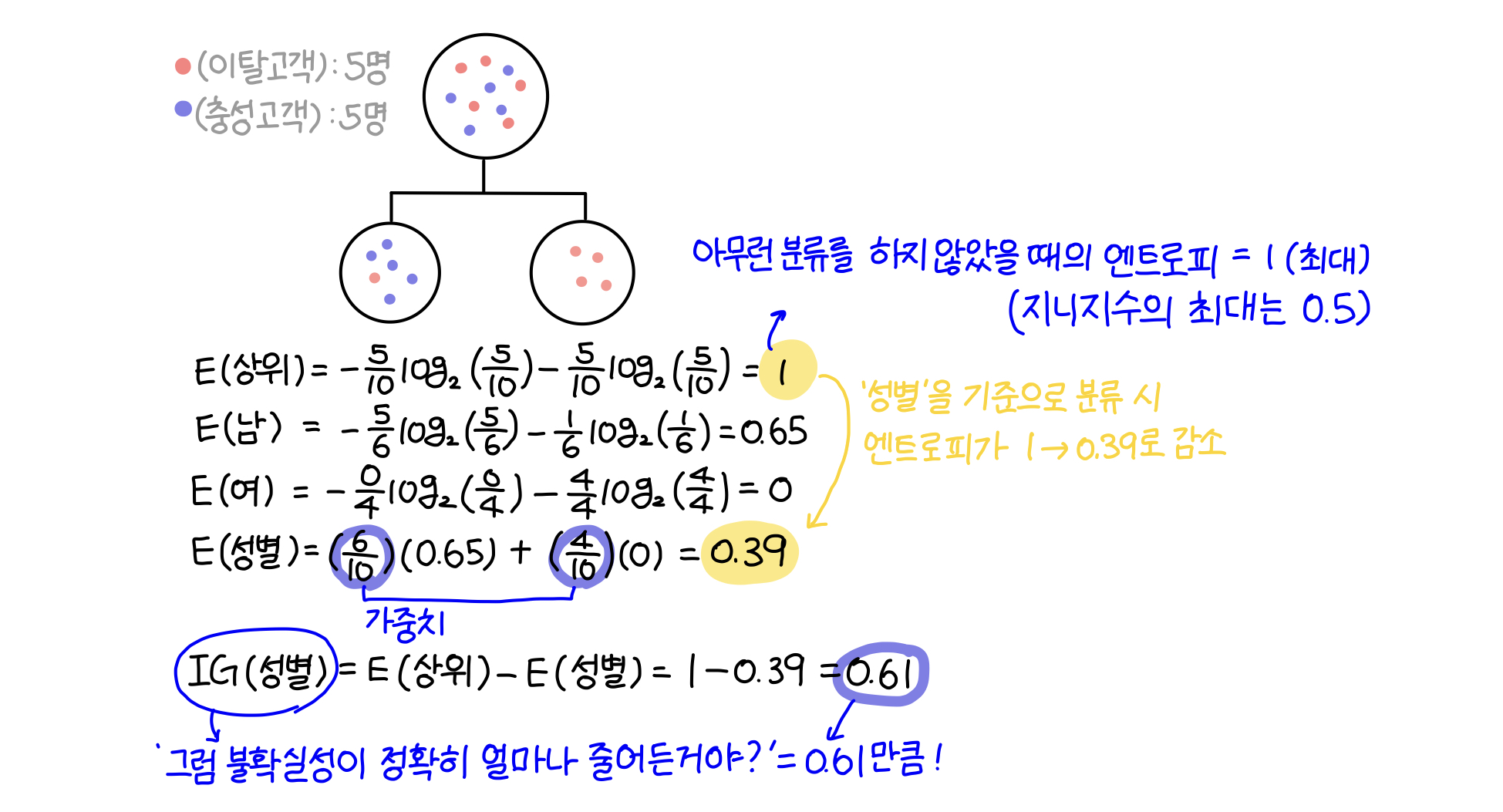
〰️ '성별'을 기준으로 분류했을 때의 엔트로피
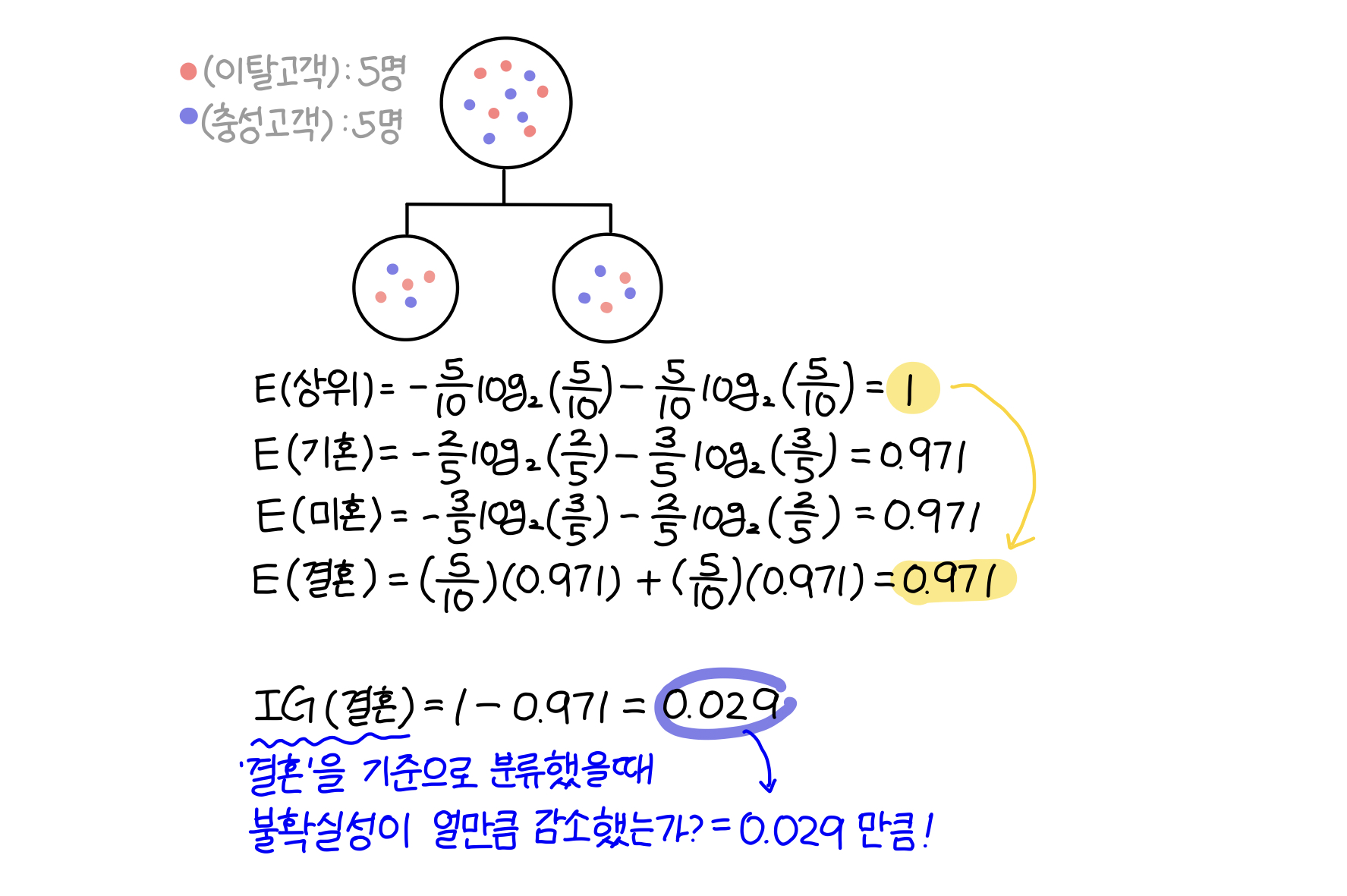
〰️ '결혼 유무'를 기준으로 분류했을때의 엔트로피
❗️결론❗️
해당 집단을 '성별'에 따라 분류했을 때는 엔트로피가 1에서 0.39으로 0.61만큼(IG) 감소했고, '결혼 유무'에 따라 분류했을때는 엔트로피가 1에서 0.971로 0.029만큼 감소했다. 따라서 이탈 고객(빨간색)을 파악하기 위해서는 '성별'에 따라 해당 집단을 분류하는 것이 좋다.



