
01. 군집 분석(Clustering analysis)
군집분석은 목표 변수(Y)가 없는 비지도 학습(unsupervised learning) 기법으로, 데이터를 구성하고 있는 객체들을 몇 개의 그룹(cluster)으로 구분하여 각 그룹들의 특성을 찾는 탐색적 분석 과정(Exploratory data analysis)이다. 이러한 클러스터링 기법을 활용하여 EDA를 시행하면 대용량 데이터에서 복잡한 관계를 이해하는 데에 도움이 되며, 고객 특성을 분류해서 고객 맞춤형 상품을 추천할 때, 패턴인식, 음성인식 등에 많이 활용된다. 하지만 비지도 학습의 특성상, 정답이 정해져 있지 않기 때문에 전체 관측치를 총 몇 개의 군집으로 구분할 것인지 또는 군집이 잘 형성되었는가에 대한 기준이 모호하다. 이에 대해서 군집 분석을 하는 분석가가 스스로 판단해야 한다는 어려움이 존재한다. 특히 연차가 낮은 분석가의 경우 이에 대한 판단이 쉽지 않을 것이다.
02. 실루엣 계수(Silhouette Coefficient)
따라서 군집분석 시 참고할 수 있는 몇 가지 지표들이 있는데, 그중 실루엣 분석 / 실루엣 계수에 대해 정리하고자 한다. 실루엣 분석은 각 군집 간의 거리가 얼마나 잘 분리 되어있는지 확인하는 분석 방법이다. 이때 군집이 '잘'분리 되어 있다는 것은 동일한 군집내의 데이터들은 가깝게 뭉쳐져있고, 다른 군집간의 거리는 멀게 형성되어 있다는 의미이다. 실루엣 분석 시 활용하는 지표로 '실루엣 계수(silhouette coefficient)'가 있는데, 실루엣 계수는 -1에서 1 사이의 값을 가지며, 1로 가까워질수록 근처에 있는 군집과 더 멀리 떨어져 있다(즉, 군집이 잘 형성되었다)는 의미고, 0으로 갈수록 군집이 잘 형성되지 않은 것이다. 또한 -1로 가까워질수록 다른 군집에 데이터가 할당되어 아예 잘못 군집이 형성되었다는 의미가 된다.
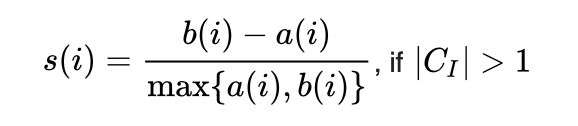
- a(i) : 해당 데이터 포인트와 같은 군집 내에 있는 다른 데이터 포인트와의 거리를 평균한 값. (군집의 응집력을 의미)
- b(i) : 해당 데이터 포인트가 속하지 않은 군집 중 가장 가까운 군집과의 평균 거리 (군집의 분리도를 의미)
좋은 군집화가 되려면 다음과 같은 기준 조건을 만족해야 한다.
- 전체 실루엣 계수의 평균값(silhouette_score())값이 0~1 사이의 값을 가지며, 특히 1에 가까울수록 좋다.
- 하지만 전체 실루엣 계수의 평균값뿐만 아니라 개별 군집의 실루엣 계수의 평균값이 전체 실루엣 계수의 평균값에서 크게 벗어나지 않는 것이 중요하다.
- 따라서 만약 전체 실루엣 계수의 평균값은 높지만, 개별 군집들의 실루엣 계수를 확인해 봤을 때 특정 군집의 실루엣 계수의 평균값만 높고, 다른 군집들의 실루엣 계수의 평균값이 낮다면 좋은 군집화 조건이 아니다.
03. 실루엣 계수(Silhouette Coefficient) 높이기 (실제 사용 예시)
이번에는 실제로 군집분석 시 실루엣 계수를 활용했던 예시를 정리하고자 한다.(실제 데이터 사용하였으며 실루엣 분석 이외의 과정은 생략 또는 간단하게 변형함)
3-1) 데이터 불러오기 및 전처리
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib as mpl
from IPython.display import set_matplotlib_formats
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
from scipy.cluster.hierarchy import dendrogram
from scipy.cluster.hierarchy import linkage
from sklearn.preprocessing import StandardScaler
mpl.rc('font', family='AppleGothic')
mpl.rc('axes', unicode_minus =True)
set_matplotlib_formats('retina')
pd.options.display.max_columns = 100
pd.options.display.max_rows = 1000
pd.options.display.max_columns = None
total = pd.read_csv('df.csv')
total.head()
사용할 데이터를 불러온 뒤, 간단히 전처리를 완료한 데이터이다.
이때 k-means 군집분석 방법을 활용하고자 범주형 데이터들은 제외하고,
연속형 데이터에 해당되는 feature들만 선택하였다.
3-2) 데이터 표준화(스케일링)
scaler = StandardScaler()
utilities_df = pd.DataFrame(scaler.fit_transform(total))
utilities_df

군집 분석은 '거리' 개념을 활용하여 각 데이터들을 군집에 할당한다. 이때 각 변수들의 스케일이 다르면 분류 영향도가 달라지므로 군집분석을 진행하기 전에 필수적으로 스케일링 작업이 필요하다.
3-3) 계층적 군집분석(Hierarchical clustering) - 덴드로그램
계층적 군집분석은 사전에 군집수(k)를 지정하지 않은 군집분석 방법이다.
이때 나는 계층적 군집분석 결과를 바탕으로 k-means기법에 군집 수를 적용하고자 해당 군집분석을 활용하였다.
Z_ward = linkage(utilities_df, method='ward', metric='euclidean')
#Z_ward
plt.figure(figsize=(10,10))
dendrogram(Z_ward, leaf_font_size=10, orientation='right')
plt.title('Hierachical Clustering Dendrogram')
plt.xlabel('distance')
plt.ylabel('sample index')method와 metric를 여러 가지 조정해 봤을 때, method='ward', metric='euclidean'으로 설정했을 때가 가장 결과가 잘 나와서 이때의 결과를 활용하였다.
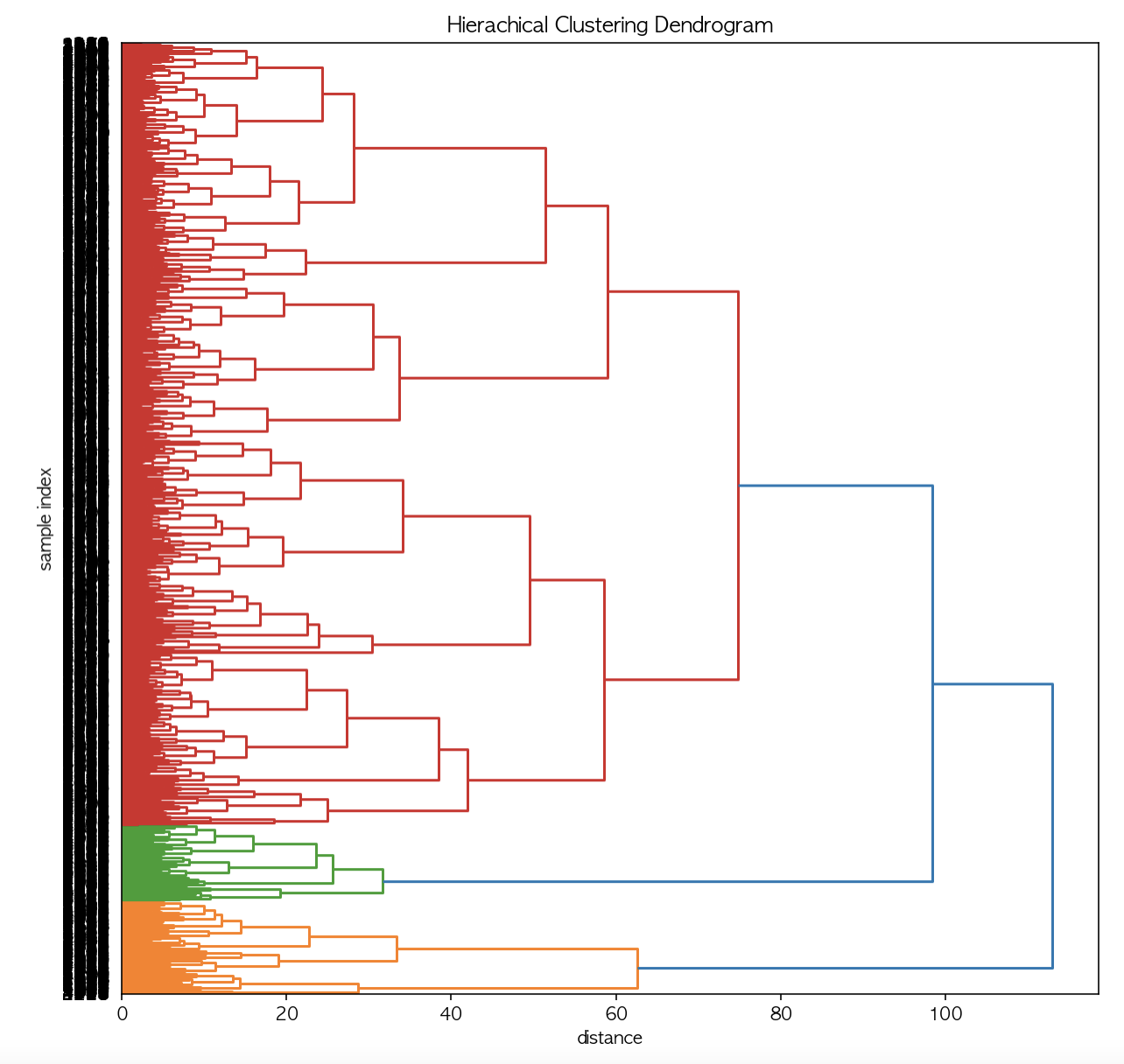
계층적 군집분석을 시행한 결과, 2개 또는 3개의 군집으로 구분하는 것이 좋을 것 같다는 생각이 들었고, k-means기법에 2 군집과 3 군집 모두 적용해보았다.
3-4) k-평균 군집분석(k-means clustering)
#k-means clustering : 3개의 군집
clus = KMeans(n_clusters=3, random_state=1111)
clus.fit(utilities_df)
cluster_kmeans = [i+1 for i in clus.labels_]
utilities_df['ClusterKmeans'] = cluster_kmeans
utilities_df
n_clustring=3으로 설정하여 전체 데이터를 총 3개의 군집으로 각각 할당하였으며, 할당된 결과는 'ClusterKmeans'칼럼을 생성하여 넣어주었다.
3-5) 실루엣 계수(silhouette_coef) 산출
total_x = utilities_df.drop(columns='ClusterKmeans')
total_y = utilities_df['ClusterKmeans']
scored_samples = silhouette_samples(total_x, total_y)
utilities_df['silhouette_coef'] = scored_samples
utilities_df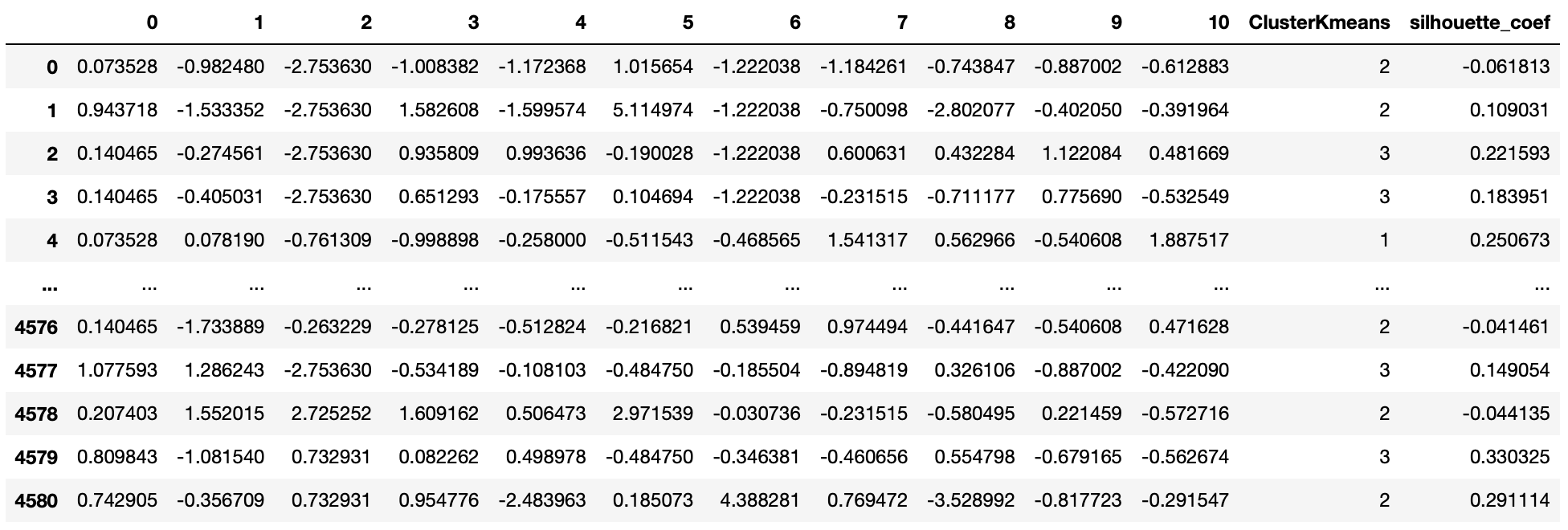
k-means의 결과를 바탕으로, 각 관측치 별 실루엣 계수를 산출했다.
3-6) 실루엣 그래프 출력
from matplotlib import cm
def silhouetteViz(n_cluster, X_features):
kmeans = KMeans(n_clusters = n_cluster, random_state = 0)
Y_labels = kmeans.fit_predict(X_features)
silhouette_values = silhouette_samples(X_features, Y_labels, metric = 'euclidean')
y_ax_lower, y_ax_upper = 0, 0
y_ticks = []
for c in range(n_cluster):
c_silhouettes = silhouette_values[Y_labels == c]
c_silhouettes.sort()
y_ax_upper += len(c_silhouettes)
color = cm.jet(float(c) / n_cluster)
plt.barh(range(y_ax_lower, y_ax_upper), c_silhouettes, height = 1.0, edgecolor = 'none', color = color)
y_ticks.append((y_ax_lower + y_ax_upper) / 2)
y_ax_lower += len(c_silhouettes)
silhouette_avg = np.mean(silhouette_values)
plt.axvline(silhouette_avg, color = 'red', linestyle = '--')
plt.title('Number of Cluster : ' + str(n_cluster) + '\n' + 'Silhouette Score :' + str(round(silhouette_avg, 3)))
plt.yticks(y_ticks, range(n_cluster)) ; plt.xticks([0, 0.2, 0.4, 0.6, 0.8, 1])
plt.ylabel('Cluster') ; plt.xlabel('Silhouette coefficient')
plt.tight_layout() ; plt.show()
silhouetteViz(3,utilities_df)
실루엣 계수를 출력해 보았을 때 현재 전체 실루엣 계수는 0.257이다. 실루엣 계수는 1에 가까울수록 군집이 잘 형성된 것이고, 0에 가까울수록 근처 군집과 가까워진다는 의미, -1에 가까울수록 군집이 엉망으로 형성되었다는 의미이다. 따라서 위의 그래프의 빨간색 점선이 1에 가까울수록 군집이 잘 형성되었다는 의미이며, 그 빨간색 선 밖으로(오른쪽)으로 데이터들이 많이 넘어가 있어야 좋은 것이다.
3-7) 실루엣 계수 높이는 방법
위의 내용까지는 기본적으로 교재나 블로그 등에 많이 기술되어 있는 내용인데, 그 이후 실루엣 계수가 낮을 때 어떻게 이를 개선해야 하는지에 대한 내용은 찾기가 어려웠다. 따라서 내가 시도했던 방법을 정리해보고자 한다. (그냥 시행착오의 기록일 뿐 정답은 아니다.)
처음 실루엣 계수를 확인했을 때 0.2 정도였고, 다양한 경우의 수로 군집을 형성해봐도 여전히 전체 평균 실루엣 계수가 0.1~0.3 정도에 머물렀다. 물론 실루엣 계수가 절대적인 지표도 아니고 도메인에 따라 다를 수 있다고 해도, 최소한 0.4~0.5이상정도 까지는 높이는게 좋을것같다고 판단했다.
〰️ 실루엣 계수(silhouette_coef)가 0보다 높은 값만 추출
cond1 = utilities_df['silhouette_coef'] > 0
df_re = utilities_df.loc[cond1]
df_re

〰️ 실루엣 계수(silhouette_coef)가 0.1보다 높은 값만 추출
cond2 = utilities_df['silhouette_coef'] > 0.1
df_re = utilities_df.loc[cond2]
df_re

〰️ 실루엣 계수(silhouette_coef)가 0.2보다 높은 값만 추출
cond3 = utilities_df['silhouette_coef'] > 0.2
df_re = utilities_df.loc[cond3]
df_re

이렇게 전체 데이터중, 실루엣계수가 각 조건에 해당되는 데이터들만 선택적으로 추출하면서 전체 평균 실루엣 계수의 변화를 확인했다.



