[머신러닝] 의사결정나무(Decision tree) -2 : CART(Classification And Regression Trees)와 지니지수(Gini index) 활용사례, 계산

5. 재귀적 분할 의사결정 알고리즘
의사결정나무에서 중요하게 알아야 할 것은 1) '어떻게 나무를 키울것인가?' 2) '불필요한 것들을 어떻게 쳐낼 것인가?'이다. 그중, 재귀적 분할 의사결정나무 알고리즘은 1)'어떻게 나무를 키울 것인가?'에 대한 내용에 해당한다. 즉 나무를 만드는 과정으로, 그 방법에는 CART, C4.5, CHAID가 있다. 또한 앞에서 정리한 내용처럼 의사결정나무에서 나무를 만들 때는 불순도가 줄어드는 방향으로 가지를 형성해나가야 하기 때문에 '불순도 알고리즘'에 대한 내용을 같이 엮어서 알아두어야 한다.
* 불순도 알고리즘 : 의사결정나무를 만들어나갈 때 클래스를 정확하게 구분해줄 수 있는 분류기준을 찾는 것이 중요하다. 즉, 이 데이터를 어떤 기준으로 분류했을때 동일한 객체들로만 잘 모아지게 할 수 있을까?를 고려해서 분류기준을 찾는것이 중요한데, 이때 불순도 알고리즘을 사용하여 현재 집단에 어느 정도 다른 객체들이 섞여있는지 확인하고 불순도가 낮은 쪽으로 가지를 형성해나가게 된다.
📌 CART(Classification And Regression Trees)
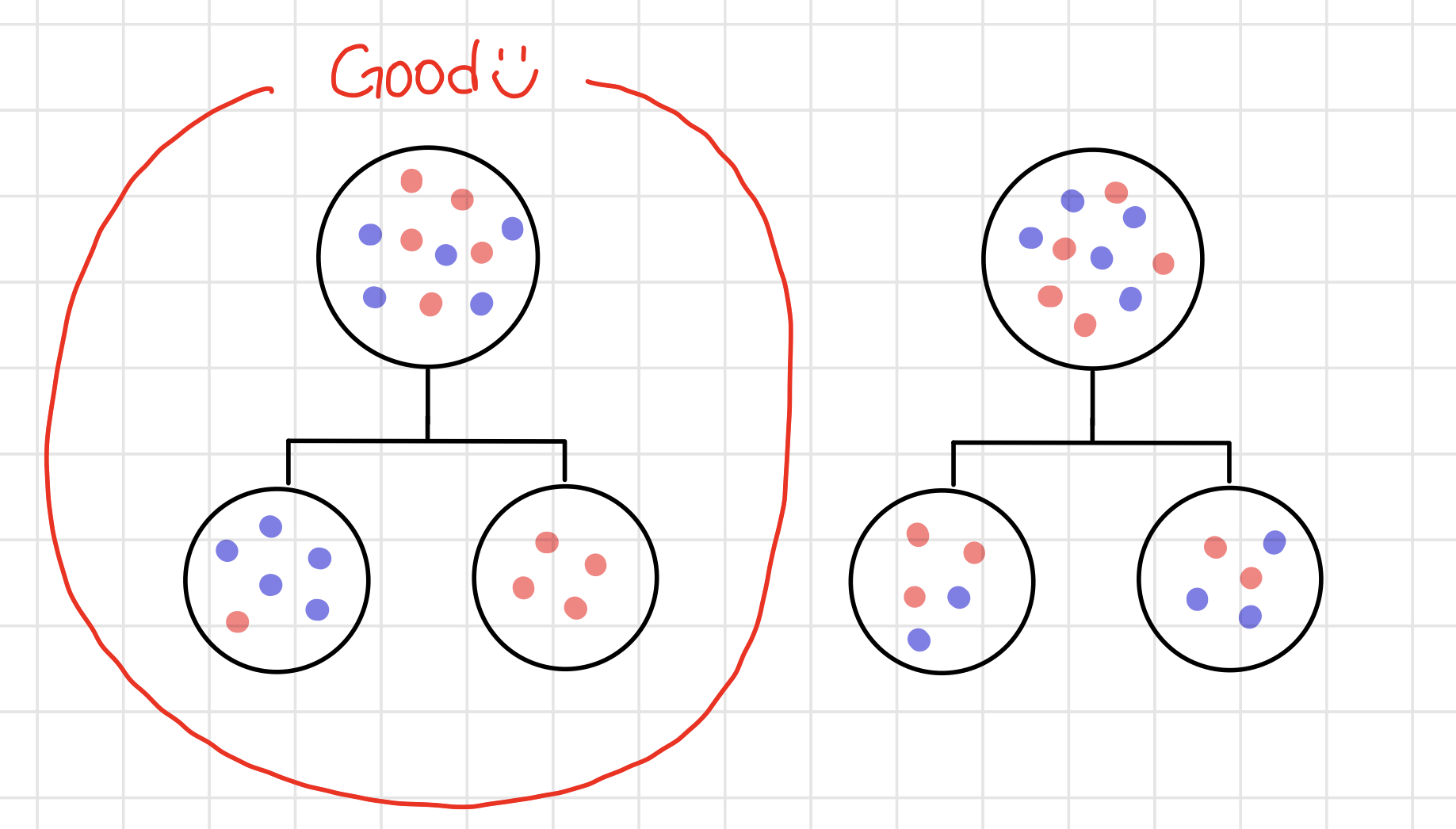
CART는 가장 널리 사용되는 의사결정나무 알고리즘으로, 이름에서도 알 수 있듯이 분류와 회귀 나무에서 모두 사용할 수 있다. 불순도를 측정할 때 목표 변수(y)가 범주형인 경우 지니 지수를 사용하고, 연속형인 경우 분산을 사용하여 이진 분리를 한다.
➰ 지니지수(Gini index)
CART에서 사용하는 불순도 알고리즘인 지니 지수는 '불확실성'을 의미한다. 즉, 지니지수는 얼마나 불확실한가? (=얼마나 많은 것들이 섞여있는가?)를 보여준다. 따라서 지니 지수가 0이라는 것은 불확실성이 0이라는 것으로 같은 특성을 가진 객체들끼리 잘 모여있다는 의미이다.
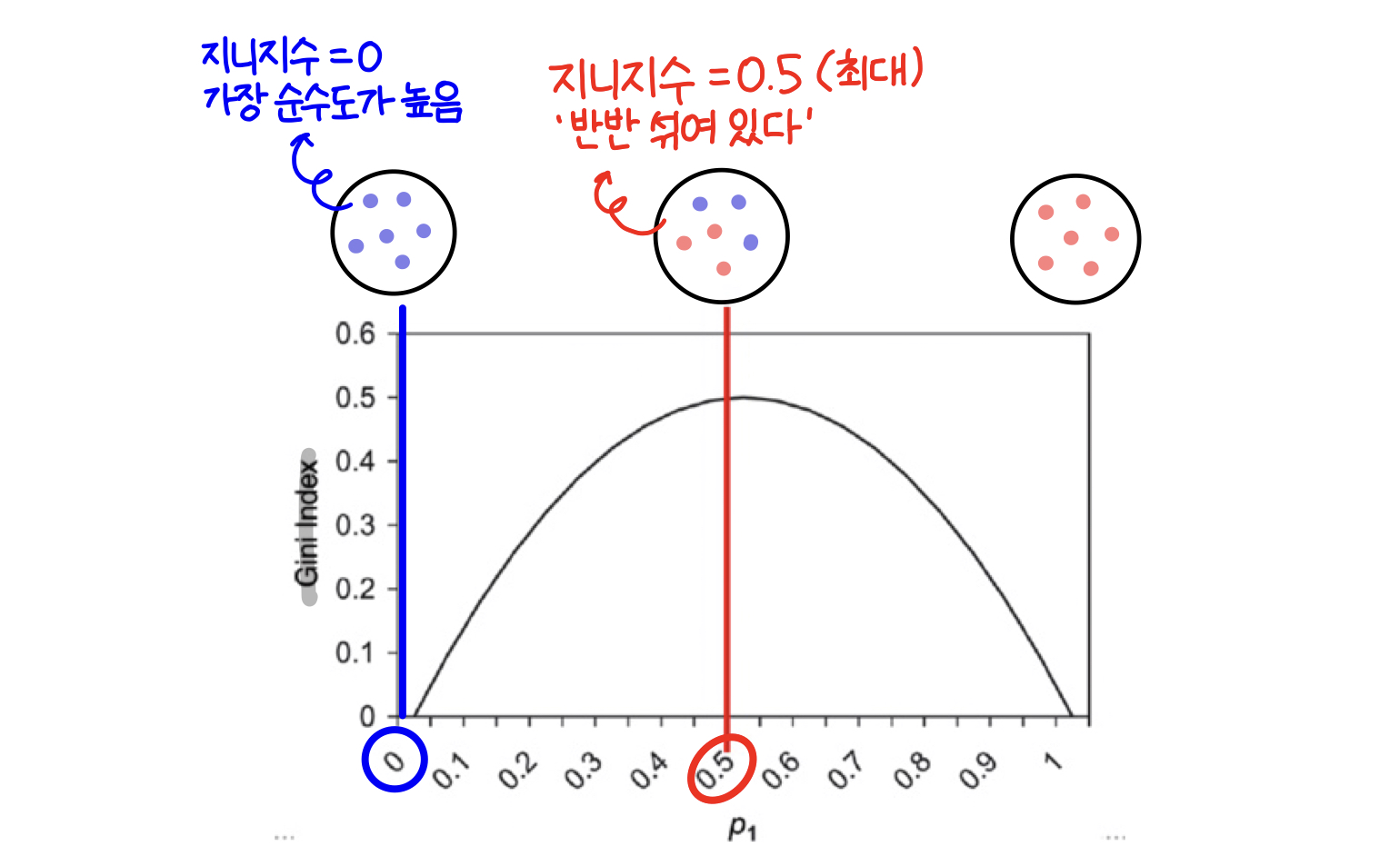
또한 지니지수는 통계학의 복원 추출 개념을 사용하기 때문에 식에 제곱이 들어간다. 한 번만 측정하는 것은 우연히 그 결과가 발생할 수 있기 때문에 최소한 두 번은 측정해봐야 정확하게 알 수 있다는 의미로 제곱을 해준다고 생각하면 된다. 어떤 집단에 한가지 특성을 가진 객체만 있을수록 그 집단을 한마디로 설명하기 좋다. 따라서 그룹 내에 있는 구성원들의 특성이 동일해질수록 지니 지수는 낮아지고, 다양한 구성원들이 섞여있을수록 지니 지수가 높아진다.

➰ 지니지수 예시
옷 쇼핑몰을 운영하고 있는 A 씨가 쇼핑몰 고객들 중, 충성고객(LC : loyal customer)과 이탈 고객(CC : churm customer)을 구분하는 규칙을 만들어서 이탈할 것으로 예상되는 고객들에게 이탈 방지를 위한 조치를 취하려 한다. 이때 총 10명의 고객을 대상으로 (성별 / 결혼 유무) 중 어느 조건(분류 기준)으로 나눠야 이탈 고객(빨간색)만 잘 분류할 수 있을지 알아보자.
〰️ '성별'을 기준으로 분류했을 때의 지니 지수

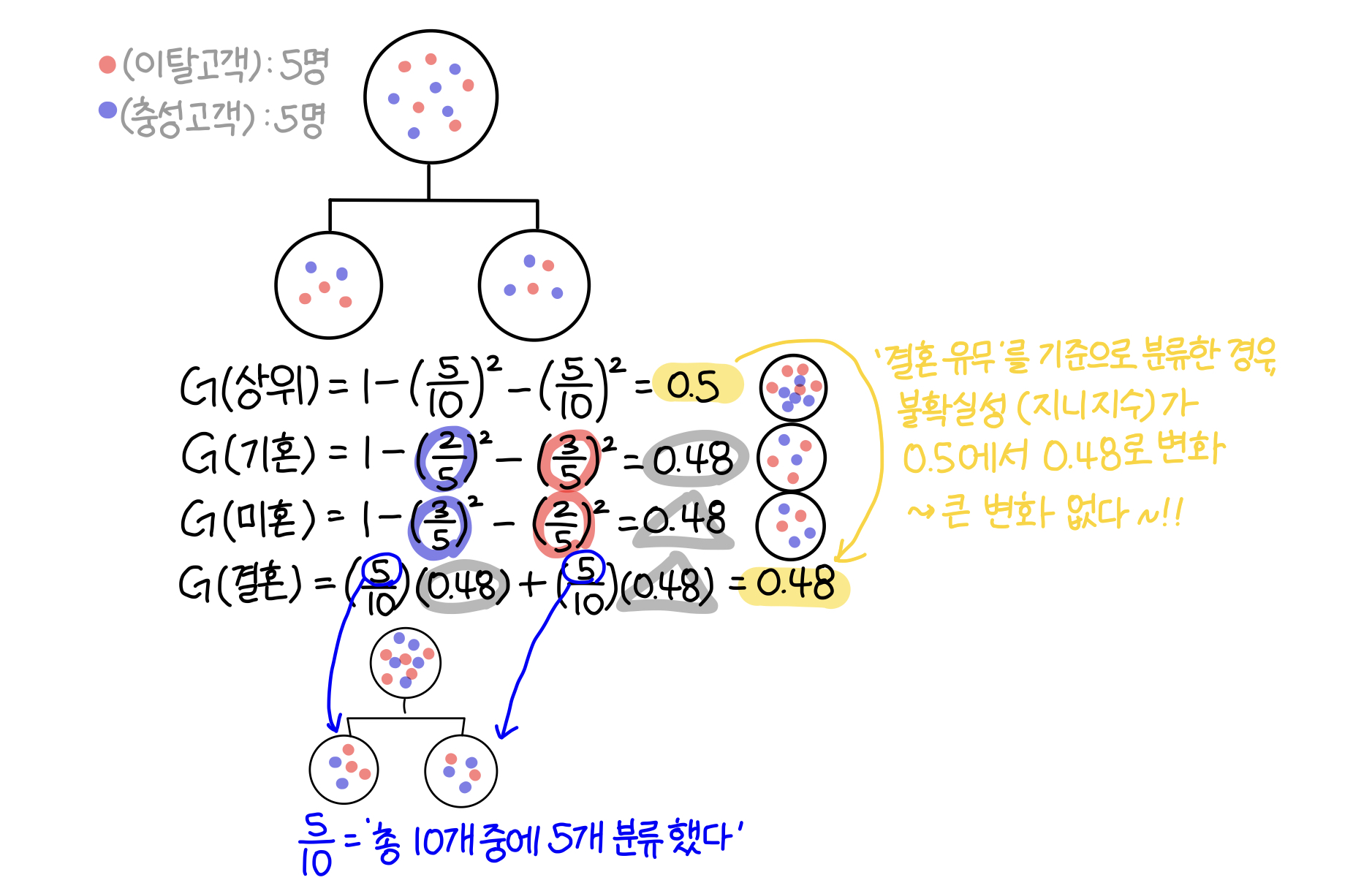
〰️ '결혼 유무'를 기준으로 분류했을때의 지니지수
❗️결론❗️
해당 집단을 '성별'에 따라 분류했을 때는 지니 지수가 0.5에서 0.167으로 감소했고, '결혼 유무'에 따라 분류했을때는 지니지수가 0.5에서 0.48로 감소했다. 따라서 이탈 고객(빨간색)을 파악하기 위해서는 '성별'에 따라 해당 집단을 분류하는 것이 좋다.