[머신러닝] 회귀(regression)-2 : 과적합(overfitting), 과소적합(underfitting), 편향 - 분산 트레이트 오프(Bias-Variance Trade off), 가중치 규제(Weight regularization)

1. 과적합(overfitting)
과적합(overfitting)이란, 모델이 학습 데이터에만 너무 잘 맞아서 새로운 데이터에 대한 예측력(일반화)이 떨어지는 것이다. 즉, 학습 데이터를 너무 과하게 학습해서 학습 데이터는 정확하게 맞추지만 실제 데이터에 대해서는 오차가 증가해서 모델을 실제로 사용하기 어려워진 것이다. 과적합은 모델의 파라미터수가 많거나 학습용(train) 데이터 세트의 양이 부족한 경우 발생한다. 특히 다항 회귀에서는 다항식의 차수가 높아질수록 매우 복잡한 피처 간의 관계까지 모델링이 가능해진다. 하지만 다항 회귀의 차수를 높일수록 과적합의 문제가 발생한다.
2. 과소적합(underfitting)
과소 적합(underfitting)은 모델이 너무 단순하여 데이터의 내재된 구조를 학습하지 못하는 것이다. 과적합이 학습용 데이터만을 너무 잘 학습해서 실제 상황에서는 쓰기 어려웠다면, 과소 적합은 학습 데이터 조차 제대로 학습하지 못한 것이다.
3. 편향 - 분산 트레이트 오프(Bias-Variance Trade off)
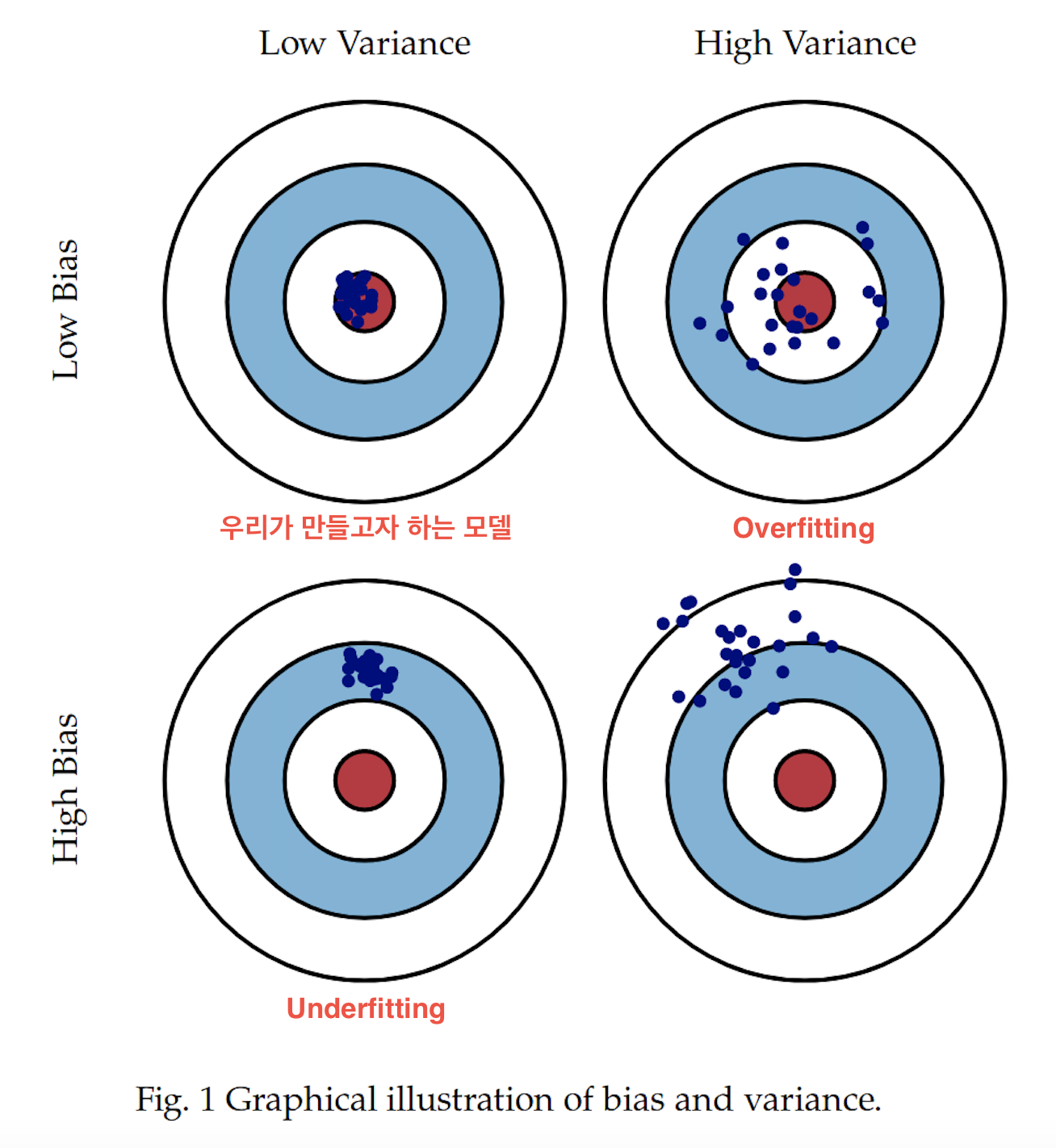
'편향-분산 트레이드오프'는 머신러닝에서 극복해야할 가장 중요한 이슈 중 하나이다. 편향(bias)는 일반화 오차중에서 잘못된 가정으로 인한것이다. 예를 들어, 실제 데이터는 2차인데 4차로 가정하는경우등에 해당되며 편향이 큰 모델은 훈련 데이터에 과소적합되기 쉽다. 분산(variance)은 훈련 데이터에 있는 작은 변동에 모델이 과하게 민감하게 반응하여 나타난다. 때문에 분산이 높을수록 과적합되는 경향이 있다.
위의 그래프에서 Low bias / Low variance는 예측 결과와 실제 결과가 매우 근접하면서도 예측 변동이 크지 않고 특정 부분에 집중되어 있으므로 모델의 성능이 아주 뛰어나다고 볼 수 있다. Low bias/ High variance는 예측 결과가 실제 결과에 비교적 근접하는 듯하지만 꽤 넓게 분포되어 있다. 이를 overfitting 된 것이라도 볼 수 있다. 즉 모든 것을 설명하려다 보니 아무것도 제대로 설명하지 못하는 현상이 나타난 것이다. 모든 데이터에 너무 민감하게 학습되어 error를 고려하지 않은 것이다. 반면 High bias/ Low variance는 underfitting이라고 볼 수 있는데, 정확한 결과값을 하나도 맞추지 못하고 특정 부분에만 예측이 집중되어 있으므로 학습 데이터가 제대로 학습되지 못했음을 의미한다. 즉, 우리가 만들었어야 하는 모델과 너무 동떨어진 상태이다.
일반적으로, 편향(bias)과 분산(variance)은 트레이드오프(trade-off) 관계로, 편향이 높아지면(과소 적합) 분산은 낮아지고 / 분산이 높으면(과적합) 편향이 낮아지는 경향이 있다.

4. 과적합(Overfitting) 방지하는 방법
1) 데이터의 개수를 늘린다.
2) Feature의 갯수를 줄인다.
3) 적절히 파라미터(Parameter)를 선정한다.
4) 가중치 규제(Weight regularization)를 적용한다.
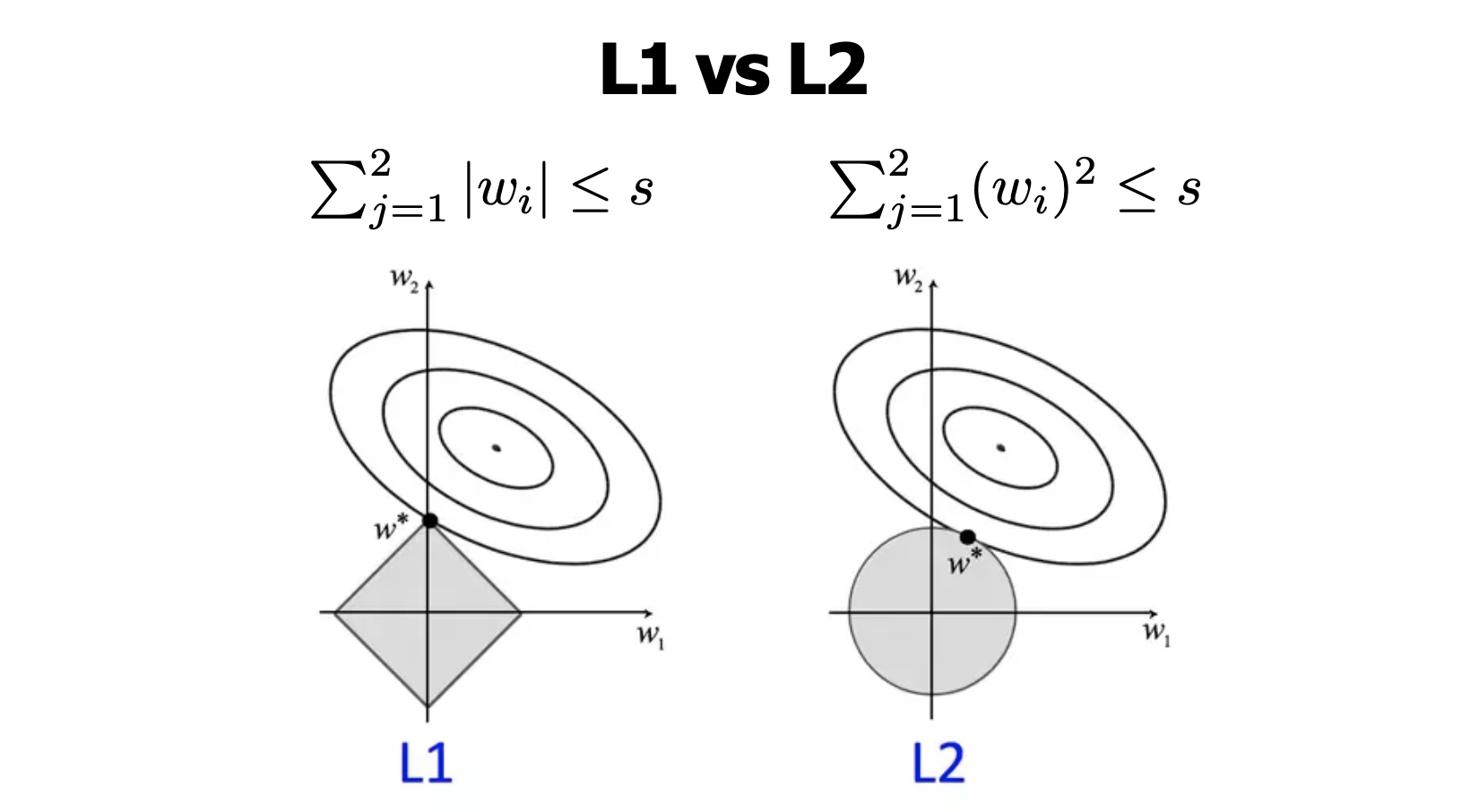
5. 가중치 규제(Weight regularization)

가중치 규제(Weight Regularization)는 많은 수의 매개 변수를 가진 복잡한 모델에 대해 과적합될 가능성을 줄이기 위해 모델을 조금 더 간단하게 만드는 방법이다. 즉, 페널티를 부여함으로써 θ의 값이 과하게 늘어나지 않도록 하는 방법이다.


가중치 규제 방법은 크게 L1 규제와 L2규제 방법으로 나눌 수 있다. 앞에서 1000을 붙여서 패널티를 줬듯 λ에 특정 수를 넣어 θ의값을 줄이는데, 이때 L1은 절댓값으로 규제를 해주고, L2는 제곱을 통해 규제를 해준다는 차이가 있다.